Understanding mixer products

How to calculate the basic produced frequencies

This article was reprinted here, after the kind permission
of the author of the rf-cafe website.

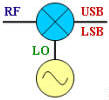
All four combinations of the mixing equation shown next to the mixer above are covered. Figures A and B, below, are equivalent results for both the LO-RF and the RF-LO cases. In case A, the subtraction results in negative frequencies, but the negative terms are said to be "reflected" or "folded" about the 0 Hz (DC) axis. The subtraction in case B does not produce any negative results, so there is no need to mathematically reflect it about the 0 Hz axis. There is no real physical reflection mechanism occurring, it is merely a mathematical convenience. The mixer has no way of determining which frequency is being subtracted from the other, regardless of how you happen to write the equation.

No spectral inversion occurs in either the upper sideband (USB) or the lower sideband (LSB) with a low-side LO injection (cases A and B). However, with a high-side LO injection, the LSB will exhibit spectral inversion while the USB does not (cases C, D and E). An explanation of spectral inversion is provided in the next paragraph. First, though, note that with a high-side LO there is an equivalent subtraction/reflection pair similar to the low-side LO case. Case E is a special case where the LO functions as both a low-side and a high-side signal. There, a portion of the band experiences spectral inversion while the other portion does not (termed "frequency folding").

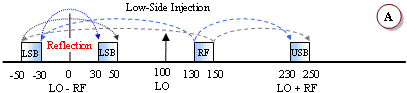
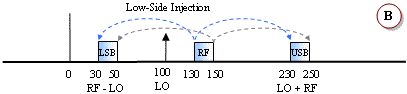
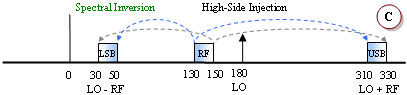
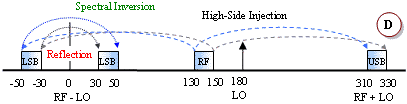
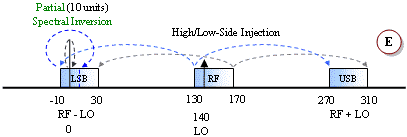
Spectral inversion occurs when the lower sideband of a high-side injected LO is used for the output, like examples C, D and E. The result is the lower frequencies of the input band being translated into the upper frequencies of the output band, and vice versa. Shading and arrow-tipped lines are used to track the relative band edges. A second inversion will cancel out the original, but a third will reintroduce the inversion, and so on. Digital systems can un-invert the spectral inversion in software or firmware if it knows to expect it. However, spectral inversion of analog voice information results in unintelligible garble. If multiple conversions are required, then an even number of inversions will result in no net inversion at the output while an odd number of inversions will always result in a net inversion at the output.

Back to main site